
- Autor Lynn Donovan [email protected].
- Public 2023-12-15 23:52.
- Última modificação 2025-01-22 17:37.
Em um losango tudo os lados são iguais e os lados opostos são paralelos. Além de um losango também é um paralelograma e, portanto, exibe propriedades de um paralelogramo e essa diagonais de um paralelogramo se dividem.
Correspondentemente, as diagonais de um losango se dividem entre si?
Em qualquer losango , a diagonais (linhas ligando cantos opostos) dividir um ao outro em ângulos retos (90 °). Isso é, cada diagonal corta o de outros em duas partes iguais, e o ângulo onde se cruzam é sempre de 90 graus. Na figura acima, arraste qualquer vértice para remodelar o losango e se convencer disso.
Em segundo lugar, as diagonais do losango são perpendiculares? Propriedades de um Losango o diagonais estão perpendicular para e dividir um ao outro. Os ângulos adjacentes são complementares (por exemplo, ∠A + ∠B = 180 °). UMA losango é um paralelogramo de quem diagonais estão perpendicular um para o outro.
Levando isso em consideração, como provar que as diagonais de um losango são bissetoras perpendiculares?
Prova que o diagonais de um losango são perpendiculares Continuação do acima prova : As partes correspondentes de triângulos congruentes são congruentes, então todos os 4 ângulos (os do meio) são congruentes. Isso leva ao fato de que eles são todos iguais a 90 graus, e o diagonais estão perpendicular um para o outro.
O losango é um paralelogramo?
DEFINIÇÃO: A losango é um paralelogramo com quatro lados congruentes. TEOREMA: Se um paralelogramo é um losango , cada diagonal divide um par de ângulos opostos. TEOREMA Converse: Se um paralelogramo tem diagonais que dividem um par de ângulos opostos, é um losango.
Recomendado:
O que é uma diagonal em um losango?
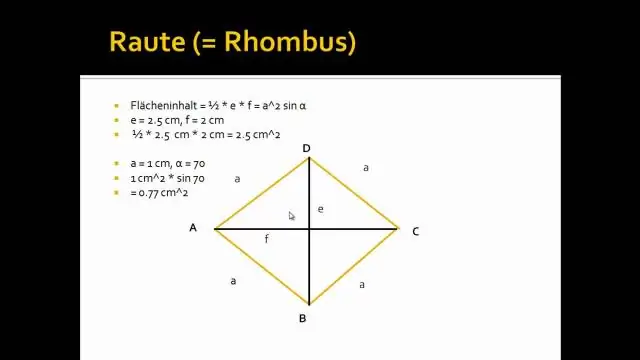
Diagonais de um losango Em qualquer losango, as diagonais (linhas ligando os cantos opostos) se dividem em ângulos retos (90 °). Ou seja, cada diagonal corta a outra em duas partes iguais, e o ângulo onde elas se cruzam é sempre 90 graus
As diagonais do quadrado são iguais?
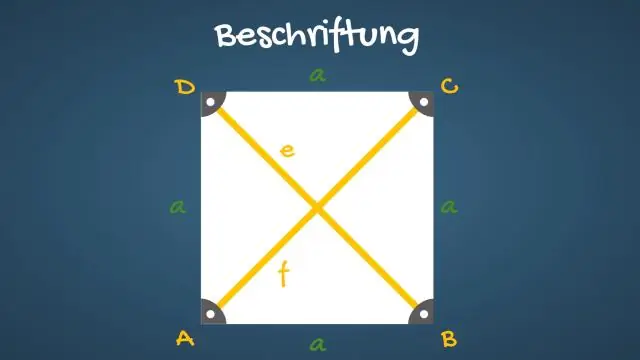
As diagonais de um quadrado dividem seus ângulos. Os lados opostos de um quadrado são paralelos e iguais em comprimento. Todos os quatro lados de um quadrado são iguais. As diagonais de um quadrado são iguais
As duas diagonais de um paralelogramo são iguais?

Quando um paralelogramo é dividido em dois triângulos, vemos que os ângulos do lado comum (aqui a diagonal) são iguais. Isso prova que os ângulos opostos em um paralelogramo também são iguais. As diagonais de um paralelogramo não têm o mesmo comprimento
As diagonais sempre se dividem entre si em um paralelogramo?
Em qualquer paralelogramo, as diagonais (linhas ligando os cantos opostos) se dividem entre si. Ou seja, cada diagonal corta a outra em duas partes iguais. Na figura acima, arraste qualquer vértice para remodelar o paralelogramo e se convencer de que é assim
Quais paralelogramos têm diagonais que se dividem?
Se dois lados adjacentes de um paralelogramo são iguais, então é um losango. Este teste é freqüentemente considerado como a definição de um losango. Um quadrilátero cujas diagonais se dividem em ângulos retos é um losango
